求矩阵的合同矩阵，怎么求合同矩阵的变换矩阵

1. 求矩阵的合同矩阵
2. 矩阵的合同标准型怎么求
3. 合同矩阵的性质
4. 矩阵合同什么意思
5. 合同矩阵需要是实对称的么

求矩阵的合同矩阵

合同矩阵是指具有相同特征值的矩阵，可以通过相似变换得到。相似变换是指通过一个非奇异矩阵P，使得合同矩阵A' = P^(-1)AP。合同矩阵具有相同的特征值和特征向量，但不一定具有相同的特征向量。合同矩阵在矩阵相似性、特征值分解等问题中具有重要应用。

矩阵的合同标准型怎么求

把主对角线上的元素都化成1就是标准型

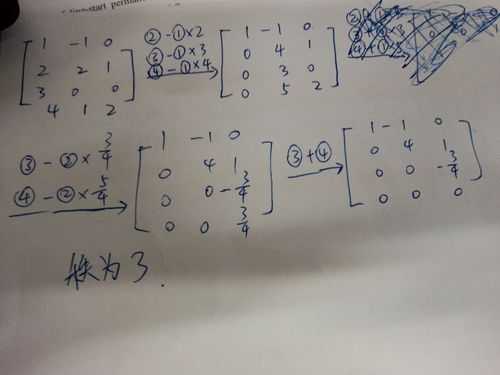
矩阵的合同标准型求的方法:

在矩阵中可画出一条阶梯线,线的下方全为0，每个台阶只有一行，台阶数即是非零行的行数，阶梯线的竖线(每段竖线的长度为一行)后面的第一个元素为非零元，也就是非零行的第一个非零元，则称该矩阵为行阶梯矩阵。

合同矩阵的性质

合同关系是一个等价关系，也就是说满足：

1、反身性：任意矩阵都与其自身合同。

2、对称性：A合同于B，则可以推出B合同于A。

3、传递性：A合同于B，B合同于C，则可以推出A合同于C。

4、合同矩阵的秩相同。

矩阵合同什么意思

“矩阵合同”可能是一个企业管理术语，它是指一种全球化范围内的管理方式，也被称为矩阵式组织、矩阵化管理。

这种管理方式是企业在组织结构上采用多种职能型、项目型、产品型、地区型等交叉组合的方式，使组织更加灵活、适应性更强，在不同的项目、产品或地区之间进行知识、技术和资源的共享与交流。

而“矩阵合同”则类似与“矩阵式合作协议”，可能指企业或组织之间的一种协作方式，以共同开展某项项目或达成某种共识为目的，也可能是一种多方合作的合同形式。

合同”是矩阵之间的一种关系.两个n阶方阵A与B叫做合同的,是说存在一个满秩n阶方阵P,使得P′AP＝B.“合同”这种关系,是一种“等价关系”.按照它可以对n阶方阵的全体进行分类.对于n阶实对称矩阵而言,线性代数中有两个结果.

①每个n阶实对称矩阵,都一定与实对角矩阵合同,并且此时P也是实的.

②对于一个n阶实对称矩阵A,与它合同的实对角矩阵当然不只一个,（相应的P也变化）.但是这些实对角矩阵的对角元中,正数的个数是一定的（叫A的正惯性指数）,负数的个数也是一定的（叫A的负惯性指数）.结果②就是“惯性定理”.

合同矩阵需要是实对称的么

合同矩阵一定是实对称矩阵。两个矩阵A和B是合同的,当且仅当存在一个可逆矩阵 C,使得C^TAC=B,则称方阵A合同于矩阵B。一般在线代问题中,研究合同矩阵的场景是在二次型中。二次型用的矩阵是实对称矩阵。两个实对称矩阵合同的充要条件是它们的正负惯性指数相同。

到此，以上就是小编对于怎么求合同矩阵的变换矩阵的问题就介绍到这了，希望介绍的5点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。

标签： 怎么求合同矩阵