矩阵的合同标准型怎么求，合同矩阵怎么求P

1. 矩阵的合同标准型怎么求
2. 如何求合同矩？如何求合同矩阵
3. 矩阵合同条件

矩阵的合同标准型怎么求

矩阵的合同标准型求的方法:

在矩阵中可画出一条阶梯线,线的下方全为0，每个台阶只有一行，台阶数即是非零行的行数，阶梯线的竖线(每段竖线的长度为一行)后面的第一个元素为非零元，也就是非零行的第一个非零元，则称该矩阵为行阶梯矩阵。

把主对角线上的元素都化成1就是标准型

如何求合同矩？如何求合同矩阵

1. 对给定的实对称矩阵A进行舒尔分解，得到A=Q^T*B*Q，其中Q是正交矩阵，B是上三角矩阵。

2. 令C=B^T，则C与A合同。

3. 如果需要求与A合同的具体矩阵，则可以对C进行一系列的初等行变换，得到一个具体的合同矩阵。

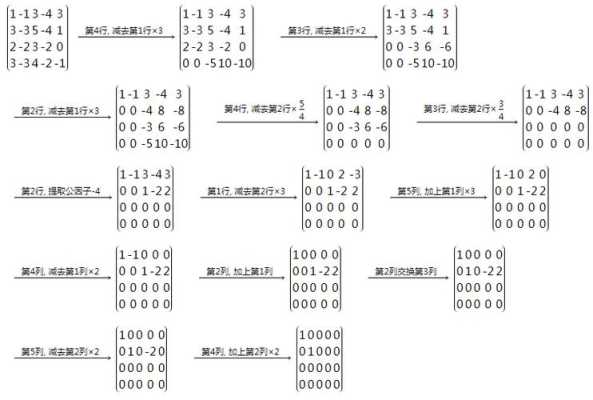
最后，需要注意的是，求解与矩阵合同的矩阵并不是一件容易的事情，需要一定的计算和技巧。同时，在计算过程中还需要注意一些细节问题，例如舒尔分解的正确性、正交矩阵的求解等等。

求合同矩阵的方法

两个实对称矩阵A和B，如存在可逆矩阵P，使得A等于P的转置乘以P乘以B，就称矩阵A和B互为合同矩阵，并且称由A到B的变换叫合同变换。合同矩阵性质：

1.

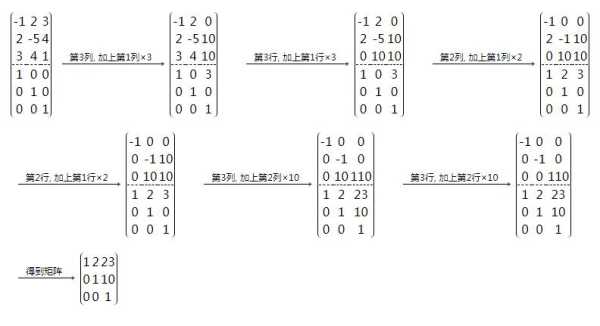
两个矩阵合同一定都是实对称阵,答案都复合。

2.

合同矩阵一定具有相同特征值,即主对角线元素相等。 在线性代数,特别是二次型理论中,常常用到矩阵间的合同关系。

您好，合同矩阵是指一个方阵，其对角线上的元素为0，其它位置上的元素根据一定的规则确定。下面是两种常见的求合同矩阵的方法：

1. 通过给定的方阵求合同矩阵：

首先，需要给定一个方阵，然后按照以下规则确定合同矩阵的元素：

- 如果两个元素在原方阵中的行和列相同，则合同矩阵对应位置的元素为0；

- 如果两个元素在原方阵中的行相同但列不同，或者行不同但列相同，则合同矩阵对应位置的元素为原方阵中对应位置的元素的相反数；

- 如果两个元素在原方阵中的行和列都不相同，则合同矩阵对应位置的元素为原方阵中对应位置的元素。

2. 通过给定的行列数求合同矩阵：

首先，需要给定合同矩阵的行数和列数，然后按照以下规则确定合同矩阵的元素：

- 对于任意的i不等于j，合同矩阵的第i行第j列的元素为1；

- 对于任意的i等于j，合同矩阵的第i行第j列的元素为0。

1. 求合同矩阵的方法有很多种，可以通过线性代数的知识进行计算。
2. 首先，合同矩阵是指一个方阵，它与其转置矩阵相等。
求合同矩阵的一种常见方法是使用特征值分解。
通过特征值分解，可以将一个矩阵分解为特征值和特征向量的乘积形式。
然后，通过对特征值进行处理， 可以得到合同矩阵的形式。
3. 除了特征值分解，还有其他方法可以求解合同矩阵，如奇异值分解、正交相似变换等。
合同矩阵在数学和工程领域有广泛的应用，例如在图像处理、信号处理和控制系统等方面都有重要的作用。

矩阵合同条件

（1）两矩阵合同的充分必要条件： 实对称矩阵A合同B的充要条件是：二次型与有相同的正、负惯性指数。

（2）两矩阵合同的充分条件： 实对称矩阵A合同B的充分条件是：因为若，则A，B具有相同的特征值，从而二次型矩阵、具有相同的标准形，即有相同的正负惯性指数，从而A与B合同。

（3）两矩阵合同的必要条件： A与B合同的必要条件是r(A)=r(B)

到此，以上就是小编对于合同矩阵怎么求P的问题就介绍到这了，希望介绍的3点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。

标签： 合同矩阵怎么求