矩阵横着拼怎么才会有解（矩阵的横向拼接）

1. 写基础解系的快速方法
2. 数学横着看和竖着看的区别
3. 视频里的人是横着的怎么竖过来
4. 矩阵的正交化和规范化

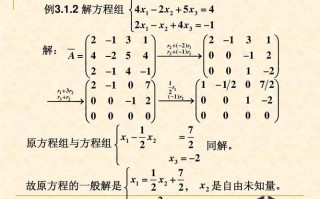
写基础解系的快速方法

基础解系可以帮助我们求解线性方程组或者研究其性质。以下是找到基础解系的一个快速方法：

1. 系数矩阵的秩：首先，我们需要计算系数矩阵的秩。秩表示了矩阵的列（或行）的线性独立性，可以帮助我们确定基础解系的维度。

2. 增广矩阵（A|b）：将系数矩阵A与常数向量b横向拼接得到增广矩阵。增广矩阵用于表示线性方程组。

3. 化简增广矩阵：通过行初等变换（如互换两行、某行乘以非零常数、某行加上另一行的若干倍等），将增广矩阵化为简化行阶梯形（Row Echelon Form，也称为简行形）。在这个过程中，我们会得到一个三角形的区域，称为基本矩阵（Baricentric Matrix）。

4. 找到基本矩阵中的非零行：在基本矩阵中，找到所有非零行（即主元行）。这些非零行对应的未知量（variables）就是基础解系的一部分。

数学横着看和竖着看的区别

数学横着看与竖着看的主要区别是视觉角度的不同。横着看时，我们更容易观察到数学问题的整体结构和关系，能够更好地理解数学概念的演绎和推理过程；竖着看时，我们更注重计算和运算的细节，能够更方便地进行数值计算和实际操作。不同的视角有助于我们全面理解和应用数学知识。

数学横着看强调数的运算和关系，如加减乘除和方程式。竖着看注重数的位值和进位，如纵向列式计算和竖式乘法。

横看重在运算过程与规律，竖看侧重于位值和进位规则，两者各有侧重点，综合起来全面展现数学的特性。

数学中横着看和竖着看通常指的是矩阵的行和列。横着看指的是沿着矩阵的行方向观察，即观察每一行的数据；竖着看指的是沿着矩阵的列方向观察，即观察每一列的数据。

以一个 2x3 的矩阵为例，横着看可以看到矩阵的第一行和第二行的数据，竖着看可以看到矩阵的第一列、第二列和第三列的数据。

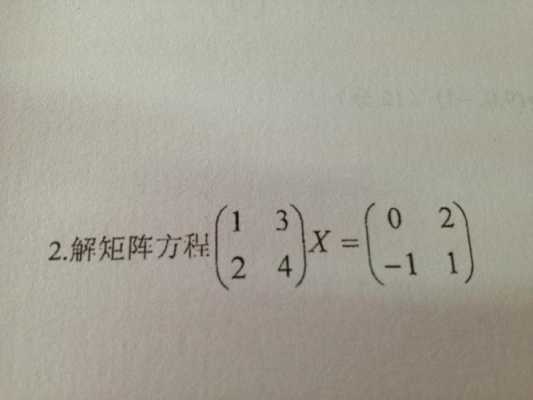
横着看和竖着看的区别在于观察的角度不同，横着看可以看到每行数据之间的关系，竖着看可以看到每列数据之间的关系。在数学中，矩阵的行和列都有其特定的含义和用途，因此根据具体的问题和需求，选择合适的观察方式可以更好地理解和处理数据。

视频里的人是横着的怎么竖过来

将横屏视频竖过来的过程被称为“旋转”。在计算机技术中，通过旋转变换矩阵来改变图像或视频中像素点的坐标，从而实现不同方向的显示。

常用软件中的旋转功能可以让使用者方便地通过简单的操作将横屏视频旋转成竖屏。但是要注意的是，由于横屏视频的比例与竖屏不同，旋转时可能会造成黑边或部分图像被截断的情况，需要进行其他编辑处理来适应不同的显示需求。

矩阵的正交化和规范化

矩阵正交化 就是存在与A行列数相同的可逆矩阵p 使得p‘Ap=E。

如果：AA'=E（E为单位矩阵，A'表示“矩阵A的转置矩阵”。）或A′A=E，则n阶实矩阵A称为正交矩阵， 若A为单位正交阵，则满足以下条件:

1) AT是正交矩阵

2)

（E为单位矩阵）

3) A的各行是单位向量且两两正交

4) A的各列是单位向量且两两正交

5) (Ax,Ay)=(x,y) x,y∈R

6) |A| = 1或-1

到此，以上就是小编对于矩阵的横向拼接的问题就介绍到这了，希望介绍的4点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。

标签： 矩阵横着拼怎么才会有解