ds怎么求S为球面（ds等于多少d单位面积）

1. 高数ds的计算公式
2. ds等于多少d单位面积

高数ds的计算公式

高数弧长ds的三种公式：s=∫ds=∫sqrt((dx)^2+(dy)^2)=∫dx*sqrt(1+(dy/dx)^2)=∫sqrt(1+f'^2(x))dx。
sqrt()是根号，()^2是()的平方。
注：ds与dx，dy是勾股关系：即dx，dy是两个直角边，ds是弧的微分，把此微弧看做直线段故ds=√(dx²+dy²)；然后将根号里的两项都除以dt²，再在根号外乘以dt就等于没乘没除了，公就是这么来的。

三种

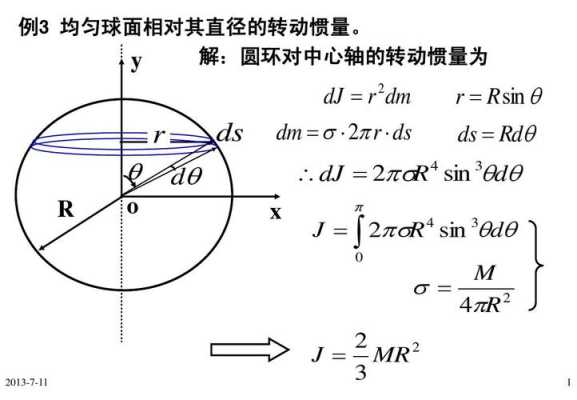
1、通用式：ds=rθ，其中r为曲线圆心与任意一点的距离，θ为曲线与x轴正向的夹角；

2、极坐标表示：ds=rθ，其中r为曲线圆心至任一点的距离，θ为终点和起点夹角；

3、直角坐标表示：ds=√[(x1-x0)2+(y1-y0)2]，其中x0、y0元素分别为曲线上起点的横纵坐标，x1、y1元素分别是曲线上终点的横纵坐标。

ds=v[(dx)十(dy)]=v[(dx)十(y)(dx)]=v[l十(y)]dx，孤长计算公式是一个数学公式，为L=nx兀xv/18O，L=axr。其中n是圆心角度数(角度制)，r是半径，L是圆心角孤长，a是圆心角度数(孤度制)

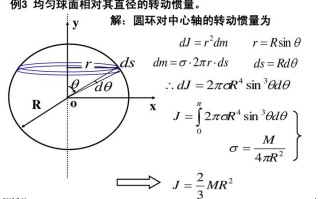
球面面积元ds公式ds=rdθ，设球半径为r,与平面xoy所成的角为θ，则面积微元是2πrcosθds，ds=rdθ。所以球面面积=2∫2πr^2*cosθdθ=4πr^2。

球体表面积是指球面所围成的几何体的面积，它包括球面和球面所围成的空间，球体表面积的计算公式为S=4πr²=πD²，该公式可以利用求体积求导来计算。

当n趋于无穷大的时候，记此时的半径差为dr，当r增量趋近于零时的增加体积dv。此时球的每层的厚度就薄的像个曲面一样，这部分很薄的体积除以dr就是球的表面积了。

在高等数学中，ds 通常表示弧微分，它可以用来计算曲线段的质量或能量。具体来说，如果用 f(x) 表示曲线段上任意一点 x 的函数值，那么 ds 就是弧微分，它可以用来计算曲线段的质量，即

f(x)ds 的积分表示曲线段的质量

其中，dx 表示曲线段上任意一点 x 的微小变化量，dy 表示曲线段上任意一点 y 的微小变化量，而 ds 则表示弧微分，它的大小为 dxdy。这个积分被称为对弧长的曲线积分，可以用来计算曲线段的质量或能量。此外，ds 也可以用来表示曲线段的长度，即

ds=sqrt(dx^2+dy^2)

其中，sqrt 表示平方根运算，dx 和 dy 表示曲线段上任意一点 x 和 y 的微小变化量。这个公式可以用来计算曲线段的长度，并且是曲线段的基本公式之一。

ds等于多少d单位面积

对于圆形来说，其面积S=πr²，

那么面积元ds就是d(πr²)，

微分就得到2πr dr

当然你也可以想象圆形的面积是其一个个圆环的周长叠加得到

每个圆环的周长为2πr，于是再乘以微元dr，

即dS=2πr dr

球面面积元ds公式ds=rdθ，设球半径为r,与平面xoy所成的角为θ，则面积微元是2πrcosθds，ds=rdθ。所以球面面积=2∫2πr^2*cosθdθ=4πr^2。球体表面积是指球面所围成的几何体的面积，它包括球面和球面所围成的空间，球体表面积的计算公式为S=4πr²=πD²，该公式可以利用求体积求导来计算。

当n趋于无穷大的时候，记此时的半径差为dr，当r增量趋近于零时的增加体积dv。此时球的每层的厚度就薄的像个曲面一样，这部分很薄的体积除以dr就是球的表面积了。

到此，以上就是小编对于球面ds等于什么的问题就介绍到这了，希望介绍的2点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。

标签： ds怎么求S为球面